In this section, we will discuss hypothesis test and confidence intervals for linear regression. Before we formally introduce the test, let’s start with some example research questions and the procedures that would be used to answer them.

Let’s consider an example, studying heart attacks in rabbits. When a heart muscle is deprived of oxygen, the tissue dies and this leads to a heart attack (myocardial infartction). Apparently, cooling the heart reduces the size of the heart attack. It is not known whether cooling the heart is only effective if it takes place before the blood flow to the heart becomes restricted. Some researchers hypothesized that cooling the heart would be effective in reducing the size of the heart attack even if it takes place after the blood flow becomes restricted.

To investigate the hypothesis, the researchers conducted an experiment on 32 anesthitized rabbits that were subjected to a heart attack. The researchers established three experimental groups:

At the end of the experiment, the researchers measures the size of the infarcted (i.e. damaged) area (in grams) in each of the 32 rabbits. But, as you can imagine, there is great variability in the size of the hearts. The size of a rabbit’s infarcted area may be large only becuase it has a larger heart. Therefore, in order to adjust for differences in heart sizes, the researchers also measured the region at risk for infarction (in grams) in each of the 32 rabits.

With their measurements in hand, the researcher’s primary question was:

Does the mean size of the infarcted area differ among the three treatment groups - no cooling, early cooling, and late cooling - when controlling for the size of the region at risk for infarction?

A regression model the researchers could use to answer their research question is:

\[y_i=\beta_0+\beta_1x_{i1}+\beta_2x_{i2}+\beta_3x_{i3}+\varepsilon_i\] where

The predictors \(x_{i2}\) and \(x_{i3}\) are called indicator variables. This translated the categorical variable treatment with three levels, early cooling, late cooling and no cooling into two dummy variables that are more useful in modeling. With these indicator variables, the model simplifies into a simpler model for each of the three experimental groups:

With this coding, \(\beta_2\) represents the difference in the mean size of the infarcted area, controlling for region at risk, between early cooling and no cooling. Similarly, \(\beta_3\) represents the difference in the mean size of the infarcted area, controlling for the size of the region at risk, between the late cooling and no cooling rabbits.

Below is a scatterplot with these three regression lines.

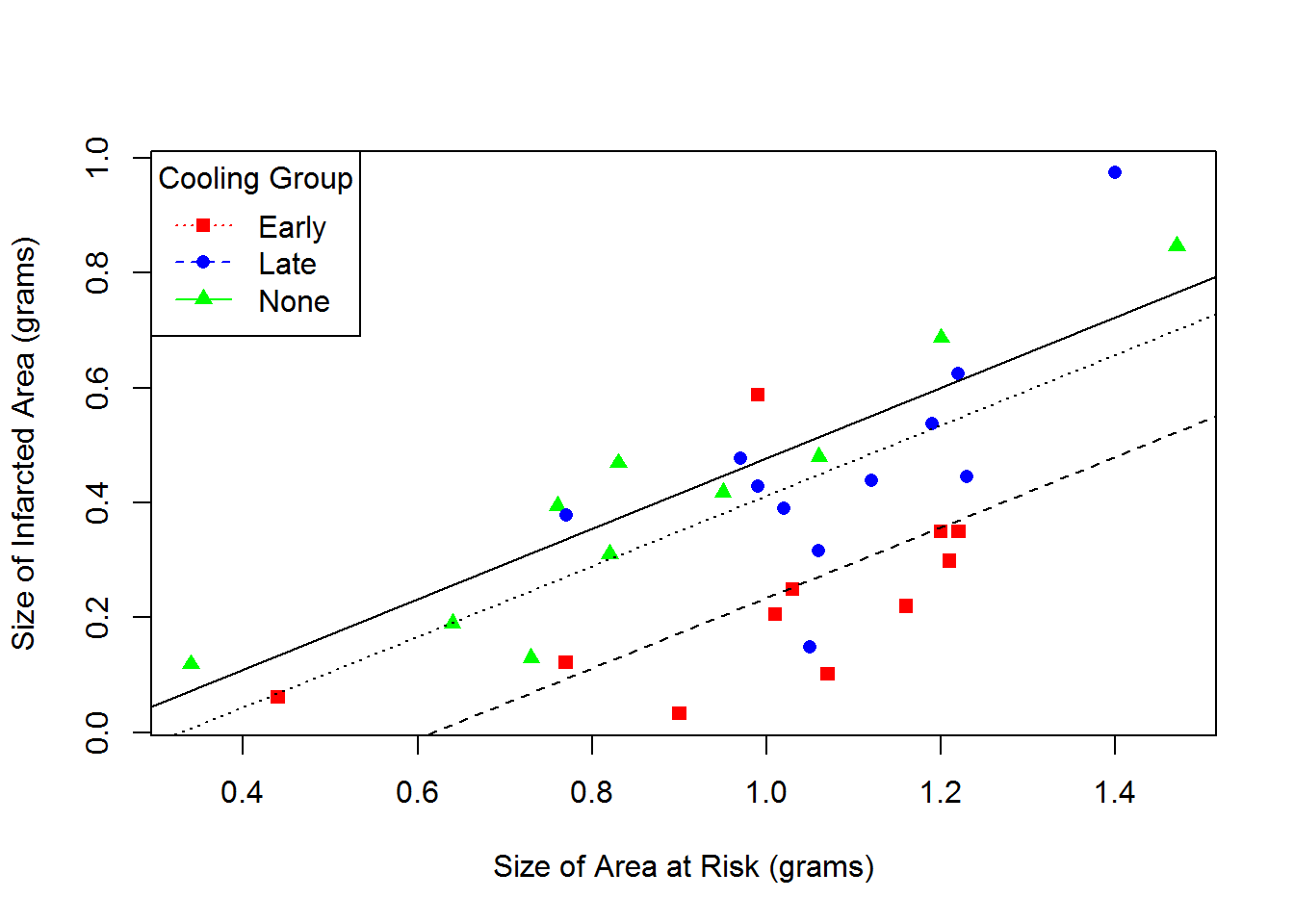From the scatterplot above, we can make the following conclusions about these 32 rabbits

But we want to draw conclusions in the population and not just about these 32 rabbits. How can we set up hypothesis tests to answer the research questions? Which confidence intervals are relevant?

Hypothesis Tests

Question 1: Are either of the predictors, size of area at risk or cooling method, useful in predicting the size of the infarcted area? This is equivalent to testing

\[H_0:\;\beta_1=\beta_2=\beta_3=0\text{ vs }H_1:\text{ At least one of $\beta_i\neq 0$ for i=1,2,3}\]

If all \(\beta_1=\beta_2=\beta_3=\), then the response \(y\) does not depend on the predictors. That is, there is no relationship between the response and predictors. If there is some relationship, then at least one of these predictors should have a non-zero slope. This hypothesis can be tested using the ANOVA F-test.

Question 2: Is the size of the infarcted area significantly (linearly) related to the type of treatment (early or late cooling) after controlling for the size of the region at risk for infarction? This can be tested by

\[H_0:\;\beta_2=\beta_3=0\text{ vs }H_1:\text{ At least one of $\beta_i\neq 0$ for i=2,3}\]

For at least one of the cooling methods to have had a significant effect on the size of the infarcted area, at least one of the slope parameters, \(\beta_2\) or \(\beta_3\), should be non-zero in this model. This can be answered using the general linear F-test.

Question 3: Is the size of the infarcted area significantly (linearly) related to the area of the region at risk? This can be answered with the following hypothesis test:

\[H_0:\beta_1=0\text{ vs }H_1:\beta_1\neq 0\] In this case, you only need to test one slope parameter. This can be done using the t-test.

The ANOVA F-test

The ANOVA F-test is used to see if any of the variables in the model are useful in predicting the response. It is based off the ANOVA decomposition. We are breaking down the total variation in y (total sum of square) into components:

  • a component that is due to the change in x (regression sum of squares)
  • a component that is just due to random error (“error sum of squares”)

If the regression sum of squares is large compared to the error sum of squares, then the regression line is doing a better job than the model with no predictors (\(\hat{y}=\bar{y}\)). The ANOVA decomposition is as follows:

\[\sum_{i=1}^n(y_i-\bar{y})^2=\sum_{i=1}^n(\hat{y}_i-\bar{y})^2+\sum_{i=1}^n(y_i-\hat{y}_i)^2\].

  • SST = SSR + SSE
  • SST has n-1 degress of freedom
  • SSR has p degrees of freedom, where p stands for the number of predictors in the model
  • SSE has \(n-p-1\) degrees of freedom

The test statistic for the ANOVA F-test is then

\[F=\dfrac{SSR/p}{SSE/n-p-1}=\dfrac{MSR}{MSE}\].

Under the null hypothesis

\[H_0: \beta_1=\beta_2=\cdots=\beta_p=0\]

the test statistic has an F distribution with numerator degrees of freedom equal to p and denominator degress of freedom equal to \(n-p-1\). The software will calculate the p-value for us.

This information is summarized in the output in an ANOVA table.

Source of Variation
DF
SS
MS
F
Regression
p
\(SSR=\sum_{i=1}^{n}(\hat{y}_i-\bar{y})^2\)
\(MSR=\frac{SSR}{p}\)
\(F^*=\frac{MSR}{MSE}\)
Residual error
n-p-1
\(SSE=\sum_{i=1}^{n}(y_i-\hat{y}_i)^2\)
\(MSE=\frac{SSE}{n-p-1}\)
 
Total
n-1
\(SSTO=\sum_{i=1}^{n}(y_i-\bar{y})^2\)
 
 

Example: Let’s return to question 1 - Are either of the predictors, size of area at risk or cooling method, useful in predicting the size of the infarcted area?

## 
## Call:
## lm(formula = Infarc ~ Area + Early + Late, data = coolhearts.dat)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.29410 -0.06511 -0.01329  0.07855  0.35949 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -0.13454    0.10402  -1.293 0.206459    
## Area         0.61265    0.10705   5.723 3.87e-06 ***
## Early       -0.24348    0.06229  -3.909 0.000536 ***
## Late        -0.06566    0.06507  -1.009 0.321602    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.1395 on 28 degrees of freedom
## Multiple R-squared:  0.6377, Adjusted R-squared:  0.5989 
## F-statistic: 16.43 on 3 and 28 DF,  p-value: 2.363e-06

For this data, \(F=16.43\) and the p-value for this test is 0.000002363. Since the p-value is very small, we have very strong evidence that at least one of the slope parameters for size of area at risk, early or late cooling is different from zero. So at least one of these variables is useful in predicting the size of the infarcted area.

General Linear F-test

The general linear F-test allows us to test if a specific subset of the variables are useful in predicting the response. The ANOVA F-test is a special case of the general linear F-test. In the ANOVA F-test, we are comparing the full model to the null model with no predictors. We can also compare the full model with a reduced model that has some but not all of the predictors. To peform this test, we need to fit both models and obtain two residual sums of square - the SSE for the full model and the SSE for the reduced model. The F-statistic in this case is:

\[F=\dfrac{(SSE(red)-SSE(full))/q}{SSE(full)/n-p-1}\],

where \(p\) is the number of predictors in the full model and \(q\) are the number of predictors we are testing to be equal to 0.

Example: Is the size of the infarcted area significantly (linearly) related to the type of treatment (early or late cooling) after controlling for the size of the region at risk for infarction? This is equivalent to testing

\[H_0:\;\beta_2=\beta_3=0\text{ vs }H_1:\text{ At least one of $\beta_i\neq 0$ for i=2,3}.\]

In this case, \(p=3\) and \(q=2\).

## Analysis of Variance Table
## 
## Model 1: Infarc ~ Area
## Model 2: Infarc ~ Area + Early + Late
##   Res.Df     RSS Df Sum of Sq      F   Pr(>F)   
## 1     30 0.87926                                
## 2     28 0.54491  2   0.33435 8.5902 0.001233 **
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

The p-value for this test is 0.001233, so there is very strong evidence that at least one of the early or late cooling treatment slopes is not equatl to zero. Therefore, there is strong evidence that the size of the infarcted area is related to the type of cooling treatment.

T-test

The t-test allows us to test if a single predictor is useful in predicting the response. For each slope parameter, we can test individually if each slope is zero or not. The hypothesis is:

\[H_0:\;\beta_i=0\;\text{ vs }\;H_1:\;\beta_i\neq 0\]

with the test statistic

\[t=\dfrac{\hat{\beta}_i-0}{SE[\hat{\beta}_i]}\overset{H_0}{\sim}t_{n-p-1}.\]

Example: Is the size of the infarcted area significantly (linearly) related to the area of the region at risk? This can be answered with the following hypothesis test:

\[H_0:\beta_1=0\text{ vs }H_1:\beta_1\neq 0.\]

## 
## Call:
## lm(formula = Infarc ~ Area + Early + Late, data = coolhearts.dat)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.29410 -0.06511 -0.01329  0.07855  0.35949 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -0.13454    0.10402  -1.293 0.206459    
## Area         0.61265    0.10705   5.723 3.87e-06 ***
## Early       -0.24348    0.06229  -3.909 0.000536 ***
## Late        -0.06566    0.06507  -1.009 0.321602    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.1395 on 28 degrees of freedom
## Multiple R-squared:  0.6377, Adjusted R-squared:  0.5989 
## F-statistic: 16.43 on 3 and 28 DF,  p-value: 2.363e-06

The p-value for this test is 0.00000387, so there is strong evidence that the slope for size of the area at risk is not equal to zero. This means that the size of the area at risk is related to the size of the infarcted area, controlling for the cooling treatment.

Confidence Intervals for the \(\beta\)’s

Confidence Interval for the Slope Parameters

If instead of testing to see if a predictor is useful in predicting the response, we want to estimate the actual effect of the predictor on the response, then we need to use confidence intervals for the slope parameters. In general, a confidence interval is of the form: estimator \(\pm\) (z or t)*standard error. For the slope parameters, the (1-\(\alpha\))100% confidence interval is:

\[\hat{\beta}_j\pm t_{\alpha/2,n-p-1}*SE[\hat{\beta}_k].\]

Example: What is the effect of the early cooling treatment on the size of the infarcted area, controlling for the size of the area at risk? We can answer this question with a confidence interval for the early cooling slope parameter.

##                  2.5 %      97.5 %
## (Intercept) -0.3476149  0.07854217
## Area         0.3933731  0.83193684
## Early       -0.3710819 -0.11588255
## Late        -0.1989419  0.06763056

The 95% confidence interval for the early cooling slope, \(\beta_2\), is (-0.37,-0.12).

  • Interpretation: We are 95% confident that the mean size of the infarcted area is between 0.12 to 0.37 grams lower for the early cooling treatment than the mean size of the infarcted area for no cooling treatment.

Confidence Intervals for the Response

If we want to estimate what the response would be for specific values of the predictors, then we can use confidence intervals for the response. There are two different confidence intervals for the response. Which one we use depends on the question of interest.

Confidence Interval for the Mean Response

The confidence interval for the mean response estimate the average of all values of the response for a given set of values of the predictors. We will not worry about the formula here. The software will do the calculations for us.

Example: What is the mean size of the infarcted area for rabbits that get early cooling and have an area at risk of size 1 g?

##         fit       lwr       upr
## 1 0.2346364 0.1484769 0.3207959

The 95% confidence interval is (0.148,0.321).

  • We are 95% confident that the mean size of the infarcted area for rabbits with area at risk of size 1 gram and who recieved the early cooling treatment is between 0.148 to 0.321 grams.

Prediction Interval

The prediction interval is still a confidence interval for the response, but instead of estimating the mean response, we are estimating the response of a new observation from the population in the future.

Example: What is the size of the infarcted area for an individual rabbit who received the early cooling treatment and has an area at risk of size 1 gram?

##         fit         lwr       upr
## 1 0.2346364 -0.06382887 0.5331016

The 95% prediction interval is given by (-0.064,0.533). Note that this interval is wider than the previous interval. This is becuase we are estimating the value of the response for a new observation and not the mean response for all observations at this level. This adds another level of uncertainty which makes the interval wider.

  • Interpretation: We are 95% confident that the size of the infarcted area for an individual rabbit in the future with area at risk of size 1 gram and who recieved the early cooling treatment is between 0.148 to 0.321 grams.

Confidence Interval for the Mean vs Prediction Interval

The key difference between these two is in what you want to estimate.

  • If you want to estimate the mean response for all subjects in the population at given levels of the predictors, then you want a confidence interval for the mean.
  • If you want to estimate the response for a single individual at given levels of the predictors, then you want a prediction interval.

Example: Determine whether you need to estimate the mean response or if you are predicting a new response in each of the following situations.

  1. A researcher is interested in answering the question: “What is the average life expectancy for individuals who smoke 2 packs of cigarettes a day?”
  2. A researcher is interested in answering the question: “What is the lung function of an individual 80-year-old woman with emphysema?”
  3. A researcher is interested in answering the question: “What is the typical weight of women who are 65 inches tall?”

Solution