In this section, we will learn how to obtain the output discussed in the notes for linear regression. At the end of this lab, you should be able to the following in R:

1. Fit a regression model with the lm function
2. Obtain the regression output with the summary function
3. Compare nested models with the anova function
4. Calculate confidence intervals for the regression slopes
5. Obtain the residual and predicted values from the lm object
6. Make new predictions and caluclate prediction intervals

For this lab, we will use the hospital infection risk dataset. Recall that this dataset contains data on hospitals to assess the infection risk with the following data on 113 hosptials:

• Response (y): The infection risk at the hospital (Percentage of patients who contract an infection while hospitalized).
• Predictor 1 (\(x_1\)): Average length of patient stay (in days)
• Predictor 2 (\(x_2\)): Average patient age (in years)
• Predictor 3 (\(x_3\)): Measure of how many x-rays are given at the hospital.

Download the dataset hospital_infct.csv by right clicking the fil and choosing Save Ling As to save the file to your computer.

First, we need to read in the data.

hospital.dat <- read.csv("Data/hospital_infct.csv",header=T)
head(hospital.dat[c("InfctRsk","Stay","Age","Xray")])

##   InfctRsk  Stay  Age  Xray
## 1      4.1  7.13 55.7  39.6
## 2      1.6  8.82 58.2  51.7
## 3      2.7  8.34 56.9  74.0
## 4      5.6  8.95 53.7 122.8
## 5      5.7 11.20 56.5  88.9
## 6      5.1  9.76 50.9  97.0

Recall the regression model for this data:

\[y_i=\beta_0+\beta_1x_{i1}+\beta_2x_{i2}+\beta_3x_{i3}+\varepsilon_i\] where

• \(y_i\) is the infection risk for hospital i
• \(x_{i1}\) is the average length of stay at hospital i
• \(x_{i2}\) is the average age of patients at hospital i
• \(x_{i3}\) is the measure of the number of x-rays given at hospital i

and the \(\varepsilon_i\) are independent and have a normal distribution with mean 0 and equal variance \(\sigma^2\). To fit this model, we will use the ‘lm’ function.

hospital.lm <- lm(InfctRsk ~ Stay + Age + Xray, data=hospital.dat)

The first argument is the formula, which in general is read \(y\sim x\). The data argument specifies the data.frame where these variables can be found. Without this argument, the lm function would throw an error, because the variable names would be undefined.

To see the output from this linear regression model, we use the ‘summary’ function.

summary(hospital.lm)

## 
## Call:
## lm(formula = InfctRsk ~ Stay + Age + Xray, data = hospital.dat)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2.77320 -0.73779 -0.03345  0.73308  2.56331 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  1.001162   1.314724   0.761 0.448003    
## Stay         0.308181   0.059396   5.189 9.88e-07 ***
## Age         -0.023005   0.023516  -0.978 0.330098    
## Xray         0.019661   0.005759   3.414 0.000899 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.085 on 109 degrees of freedom
## Multiple R-squared:  0.363,  Adjusted R-squared:  0.3455 
## F-statistic:  20.7 on 3 and 109 DF,  p-value: 1.087e-10

If we wanted to add an interaction term betweem age and length of stay, we would need to add the term ‘Age:Stay’ to the original model formula or to use the short cut ’Age*Stay’. The shortcut is equal to ‘Age + Stay + Age:Stay’.

hospital.lm2 <- lm(InfctRsk ~ Stay + Age + Xray + Stay:Age, data=hospital.dat)
summary(hospital.lm2)

## 
## Call:
## lm(formula = InfctRsk ~ Stay + Age + Xray + Stay:Age, data = hospital.dat)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2.77573 -0.73640 -0.02913  0.78514  2.60569 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -2.650216   6.262824  -0.423   0.6730    
## Stay         0.679877   0.626080   1.086   0.2799    
## Age          0.042410   0.112191   0.378   0.7062    
## Xray         0.020065   0.005815   3.450   0.0008 ***
## Stay:Age    -0.006696   0.011228  -0.596   0.5522    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.088 on 108 degrees of freedom
## Multiple R-squared:  0.3651, Adjusted R-squared:  0.3416 
## F-statistic: 15.53 on 4 and 108 DF,  p-value: 4.603e-10

# The following will result in the same model and output
# hosptial.lm2 <- lm(InfctRsk ~  Xray + Stay*Age, data=hospital.dat)

All of the regression information for the fitted model is stored within the lm object. To see what components are contained in the lm fit, we can use the ‘names’ function.

names(hospital.lm)

##  [1] "coefficients"  "residuals"     "effects"       "rank"         
##  [5] "fitted.values" "assign"        "qr"            "df.residual"  
##  [9] "xlevels"       "call"          "terms"         "model"

We can extract the individual peices by referencing the named parts. The lm object is a list with each of these named components. There are also helper functions for some of the most commonly used parts.

hospital.lm$coefficients #use the dollar sign operator to reference the component

## (Intercept)        Stay         Age        Xray 
##  1.00116169  0.30818090 -0.02300522  0.01966093

coef(hospital.lm) #use the coef helper function

## (Intercept)        Stay         Age        Xray 
##  1.00116169  0.30818090 -0.02300522  0.01966093

Other helpful functions for the lm object are ‘residuals’, ‘fitted’, and ‘vcov’ which extract the residuals, fitted (or predicted) values and the variance-covariance matrix of the \(\beta\)’s respectively. For example, to make the scatterplot of residuals vs fitted

resid <- residuals(hospital.lm) #get the residuals
pred.values <- fitted(hospital.lm) #get the fitted values
plot(pred.values,resid,xlab="Predicted Values",ylab="Residuals",pch=16)
abline(h=0)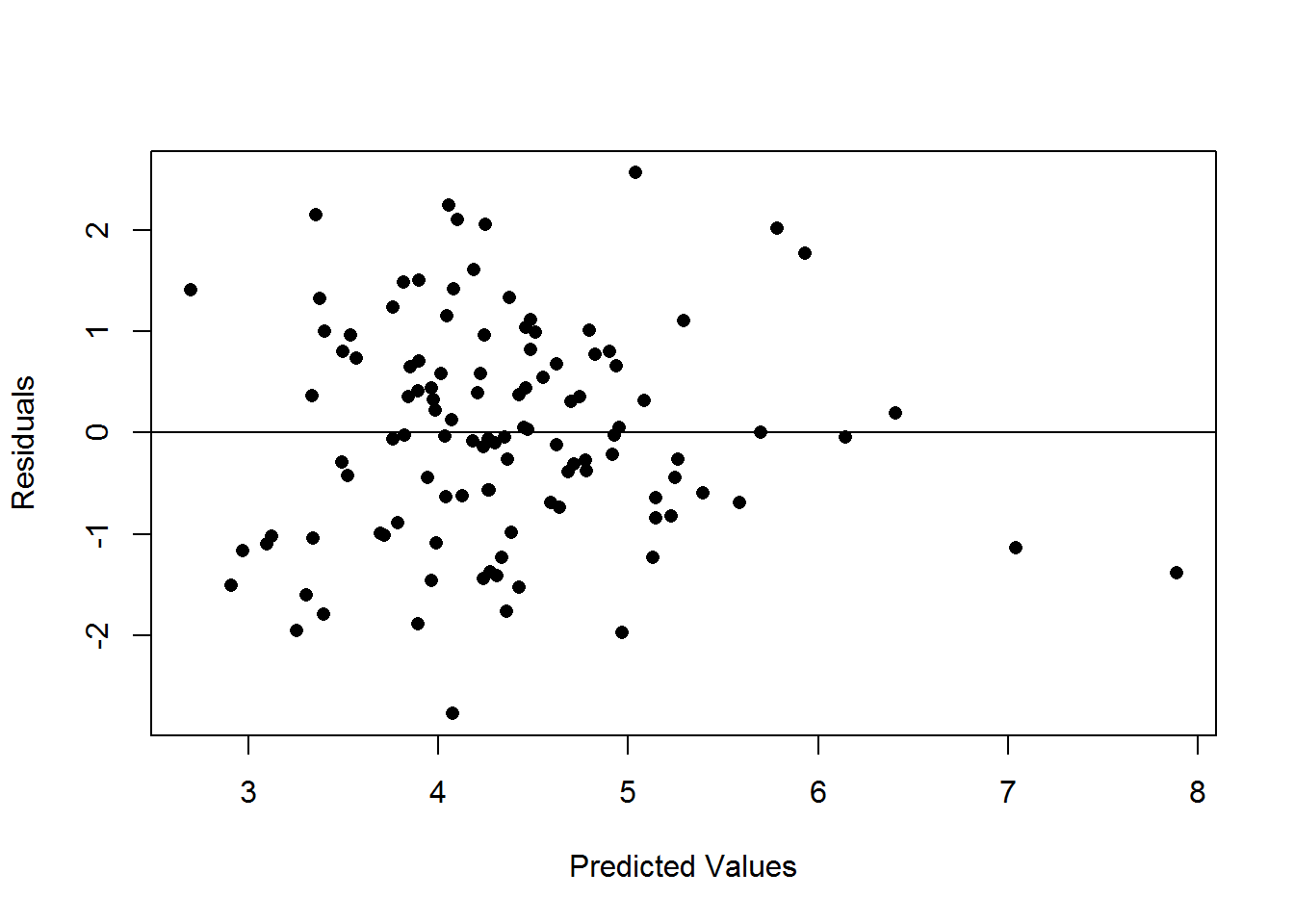

To perform the general linear F-test, you need to fit the full and reduced models and then apply the ‘anova’ function to these two lm objects. For example, if we wanted to test to see if the interaction term was significant (we could just look at the t-test) using the general F-test, we would use the following code:

anova(hospital.lm,hospital.lm2)

## Analysis of Variance Table
## 
## Model 1: InfctRsk ~ Stay + Age + Xray
## Model 2: InfctRsk ~ Stay + Age + Xray + Stay:Age
##   Res.Df    RSS Df Sum of Sq      F Pr(>F)
## 1    109 128.28                           
## 2    108 127.86  1   0.42109 0.3557 0.5522

The interaction is not significant.

Confidence intervals for the regression slopes are obtained by using the ‘confint’ function.

confint(hospital.lm, level=0.95)

##                    2.5 %     97.5 %
## (Intercept) -1.604578161 3.60690155
## Stay         0.190460657 0.42590115
## Age         -0.069612730 0.02360229
## Xray         0.008247657 0.03107420

The default confidence level is 95%, but this can be changed by using the level argument.

To make predictions and get the confidence intervals for the mean and predition intervals, use the R function ‘predict’. We need to specify the values of the predictors by specifying them in a data.frame with columns having the exact same names as those used in the model.

print("Fitted Value")

## [1] "Fitted Value"

predict(hospital.lm,data.frame(Age=55,Stay=10,Xray=89)) #get the fitted value for these values (y-hat)

##        1 
## 4.567506

print("Confidence interval for the mean response")

## [1] "Confidence interval for the mean response"

predict(hospital.lm,data.frame(Age=55,Stay=10,Xray=89),interval="confidence") #get the confidence for the mean response

##        fit      lwr     upr
## 1 4.567506 4.335773 4.79924

print("Prediction Interval")

## [1] "Prediction Interval"

predict(hospital.lm,data.frame(Age=55,Stay=10,Xray=89),interval="prediction") #get the prediction interval

##        fit      lwr      upr
## 1 4.567506 2.404927 6.730085

The confidence level can be adjusted with the ‘level’ option. The defualt is 95%.