Simple Linear Regression

Deterministic vs Statistical Relationships

In algebra, we learn about the equation of a line

\[y=mx+b\]

where

• m is the slope
• b is the y-intercept.

In deterministic relationships, all the points fall exactly on the line, becuase the x-value completely determines the y-value. As an example, consider the deterministic linear relationship between degress celsuis and degrees fahrenheit:

\[F=\dfrac{9}{5}C+32\]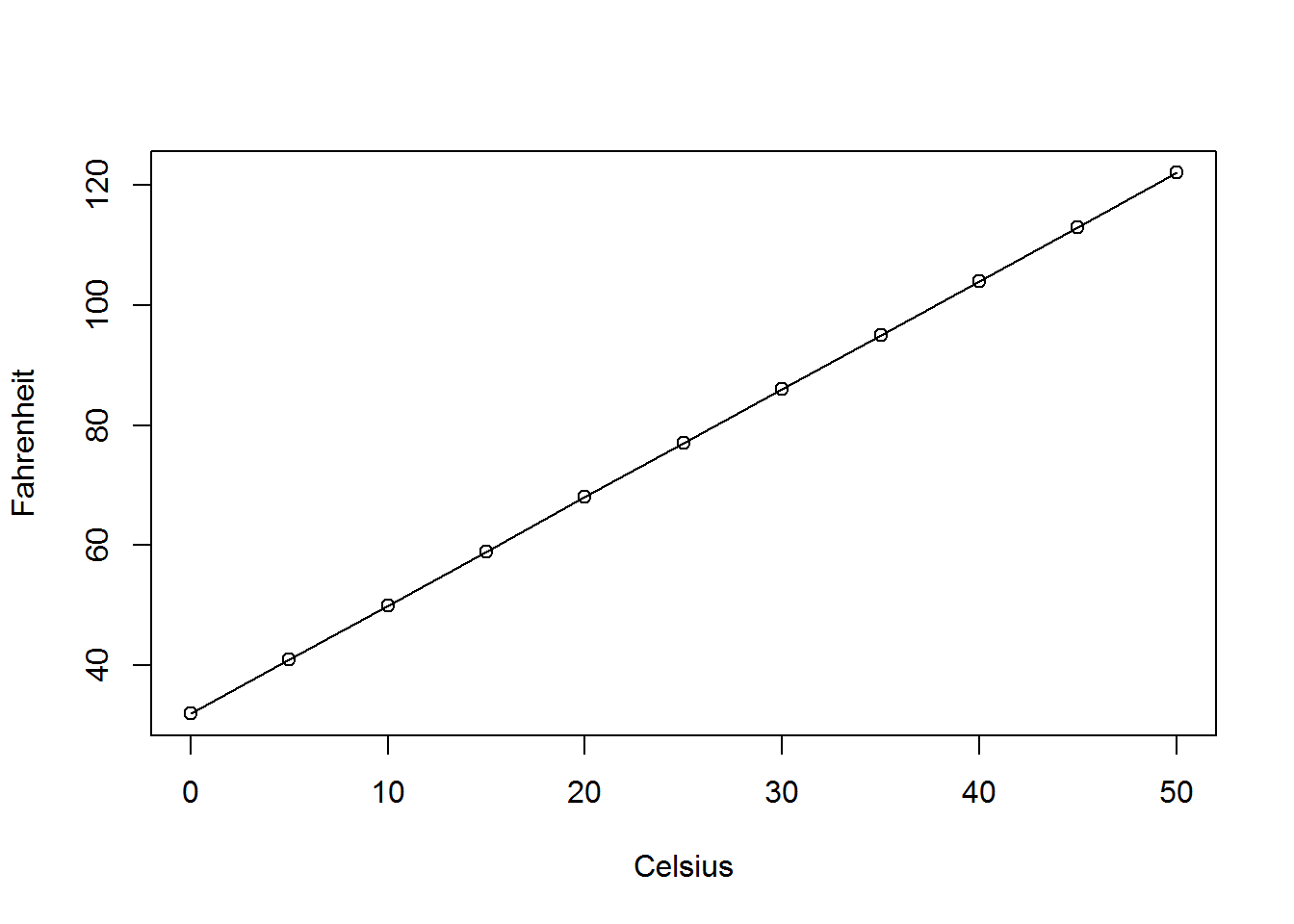

If you know the temperature in degrees Celsius, then you know the temperature in degrees Fahrenheit. There is no error in the relationship. You can determine one from the other exactly.

In statistical relationships, the relationship between the predictor and response is not perfect. This could be due to many factors such as measurement error or factors that are not accounted for in the model that also determine the response value. As an example, consider skin cancer mortality and latitude (this measures from North to South) in the United States by state. It is reasonable to assume that if you live at higher latitudes (further North), then you are less exposed to harmful sun rays, and therefore, have a lower risk of death due to skin cancer. Therefore, we expect a decreasing relationship, but we do not expect the moratlity rate to be completely determined by the latitude. As we see in the scatterplot below, there is a negative linear trend, but the points scatter around this line.

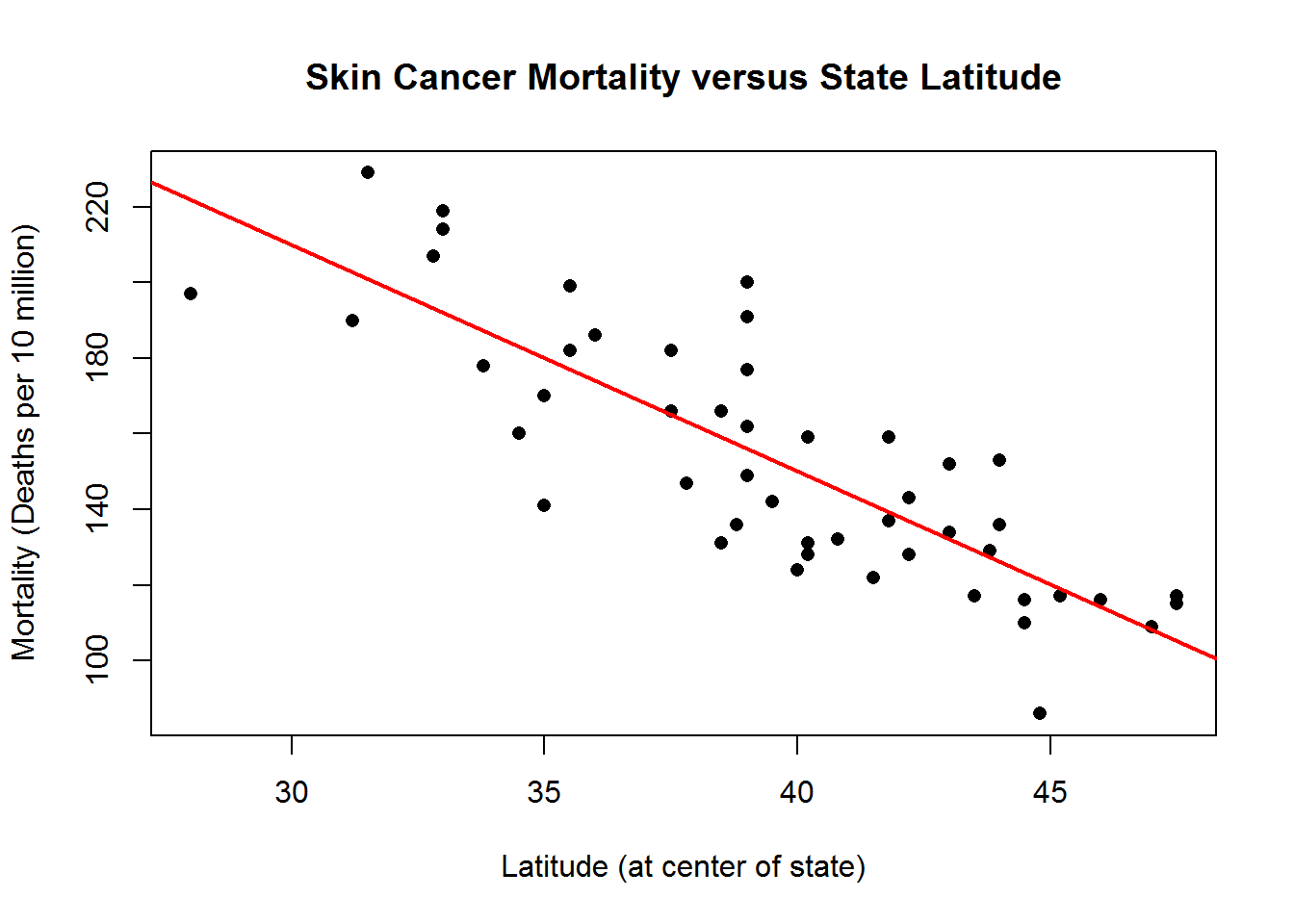
Some other examples of statistical relationships might include:

• Height and weight - as height increases, you’d expect weight to increase, but not perfectly.
• Alcohol consumed and blood alcohol content - as alcohol consumptions increases, you’d expect one’s blood alcohol content to increase, but not perfectly.
• Vital lung capacity and pack-years of smoking - as amount of smoking increases (as quantified by the number of pack-years smoking), you’d expect lung function (as quantified by vital lung capacity) to decrease, but not perfectly.

Best Fitting Line

Our goal is to summarize the relationship between the two variables with a line, but if you look at a scatterplot there are many lines that fit through the data. How do we pick the line?

Suppose we have chosen a line and let \(\hat{y}_i\) be the value of \(y\) on this line for \(x_i\). This is the predicted (or fitted) value of the response for this value of the predictor. With this prediction, we make a prediction error (or residual error)

\[e_i=y_i-\hat{y}_i\].

The residuals are the vertical distance from the observed y to the predicted y-value on the regression line.

The line that best fits the data should minimize this prediction error. The criterion we will use for linear regression is the least squares criterion. We will choose our line as the line that minimizes the sum of squared predcition errors. For simple linear regression, we want to find a line of the form

\[y=\beta_0+\beta_1x\]

• The best fitting line is \(\hat{y}=\hat{\beta_0}+\hat{\beta}_1x\). Note that we have “hats” on y and the beta’s becuase these are estimates of the linear relationship.
• We need to find the \(\hat{\beta}_0\) and the \(\hat{\beta}_1\) that make the sum of square prediction errors as small as possible. That is, to minimize:

\[\begin{align}Q &= e_1^2+e_2^2+\cdots+e_n^2\\ &=(y_1-\hat{y}_1)^2+(y_2-\hat{y}_2)^2+\cdots+(y_n-\hat{y}_n)^2\\ &=\sum_{i=1}^n(y_i-\hat{\beta}_0-\hat{\beta}_1x)^2\end{align}\]

Note: The symbol \(\sum_{i=1}^n\) means to add all the terms.

For simple linear regression, the criterion leads to the following estimates:

• \(\hat{\beta}_1=r\dfrac{s_y}{s_y}=\dfrac{\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})}{\sum_{i=1}^n(y_i-\bar{y})^2}\)
• \(\hat{\beta}_0=\bar{y}-\hat{\beta}_1\bar{x}\)

Note: Do not worry about these formulas. We will use a software package to perform the calculation for us.

The Simple Linear Regression Model

What does this least square regression line estimate? Recall the skin cancer example. Note that we can have more than one observed value for skin cancer mortality for the same latitude, but a line is a function that can only take a single value. So instead of the observed value, let’s consider the mean mortality rate for a given latitude. The average of all the moratlity rates at a given latitude is a single value. This is what we are modeling:

\[E(Y_i|x)=\beta_0+\beta_1x.\]

The formal simple linear regression model is as follows:

\[y_i=\beta_0+\beta_1x_i+\varepsilon_i\]

where \(\varepsilon_i\) are independent and normally distributed with mean 0 and variance \(\sigma^2\). The error term is a “catch-all” term for what we miss in the model: the true relationship is probably not linear, there may be other varaiables that cause changes in \(Y\), and there may be measurement error.

Interpretation for the parameters:

• \(\beta_1\) - This is the slope. This represents the mean change in the outcome y for a one unit change in x.
• \(\beta_0\) - This is the y-intercept. This represents the mean value of the outcome, y, when x=0. The y-intercept should only be interpreted if x=0 makes sense and we have observed data with x-values near 0.

The assumptions of this model can be summarized by the word LINE:

• The mean of the response at each value of the predictor, \(x_i\), is a Linear function of the \(x_i\).
• The errors, \(\varepsilon_i\), are Independent.
• The errors, \(\varepsilon_i\), are Normally distributed.
• The errors, \(\varepsilon_i\), have Equal variances.

Pearson’s Correlation and the Coefficient of Determination

Pearson’s correlation coefficent, denoted by \(r\), is a measure of the strength and direction of the linear relationship between the response and (the single) predictor. Pearson’s correlation has the following properties:

• r is between -1 and 1: \(-1\leq r\leq 1\).
• \(r=-1\) if there is a perfectly negative linear relationship between x and y.
• \(r=1\) if there is a perfectly positive linear relationship between x and y.
• \(r=0\) if there is no linear relationship between x and y.

The closer r is to 1 or -1, the stronger the linear relationship. The close r is to 0, the weaker the linear relationship. Below are some example scatterplots with the corresponding r values.

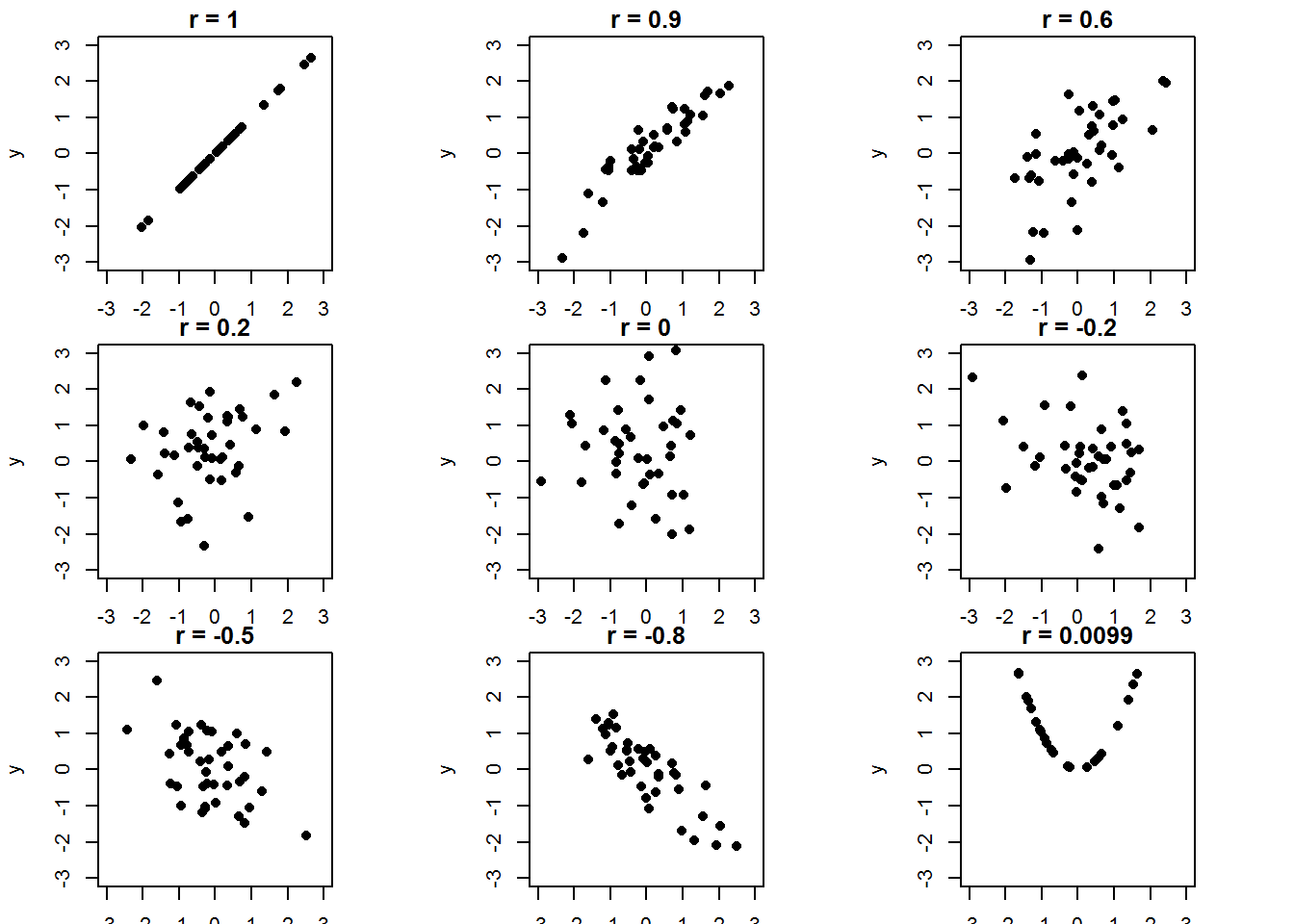
Note that in the last plot, there is a very strong quadratic relationship relationship between x and y. If we just look at r, then we would make the wrong conlcusion that there is a weak linear relationship. It is important to check your data to see if there is a linear relationship.

The coefficient of determination, \(R^2\), is a measure of how well the model fits the data. Recall that \(R^2=r^2\).

• Interpretation: \(R^2\) is the percent of the variablity in the outcome, \(y\), explained by the linear regression model using \(x\).

• Higher \(R^2\) means that your model has more predictive power for the response.