Example: Multiple Linear Regression
Now that we have covered the major concepts in multiple linear regression, let’s work through an example.
Example: Risk Factors for Heart Disease
Body mass index (BMI) and low density lipoprotein (LDL) cholesterol are both known risk factor for CHD. It is reasonable to hypothesize that higher BMI leads to higher LDL, but this association may be depend on other factors such as age, ethnicity, smoking, statin use (statins are a class of drug used to lower cholesterol levels) and alcohol use. These other factors might also have a relationship with LDL cholesterol as well. Data was collected in an observational study of women. Consider the following regression model:
\[y_i=\beta_0+\beta_1x_{i1}+\beta_2x_{i2}+\beta_3x_{i3}+\beta_4x_{i4}+\beta_5x_{i5}+\beta_{6}x_{i6}+\beta_{56}x_{i5}x_{i6}+\varepsilon_i\]
where
- \(y_i\) is the LDL cholesterol level of patient i in mg/dL
- \(x_{i1}\) is the age in years of patient i
- \(x_{i2}=1\) if the patient i is non-white, and is 0 otherwise
- \(x_{i3}=1\) if the pateint i smokes and 0 otherwise
- \(x_{i4}=1\) if the patient i drinks alcoholic beverages
- \(x_{i5}\) is the BMI of patient i
- \(x_{i6}=1\) if the patient uses statins and is 0 otherwise
and the \(\varepsilon_i\) are independent and have normal distributions with mean 0 and equal variance \(\sigma^2\).
First, let’s fit this regression model.
##
## Call:
## lm(formula = LDL ~ age + nonwhite + smoking + drinkany + BMI *
## statins, data = hers.dat, subset = drinkany != "")
##
## Residuals:
## Min 1Q Median 3Q Max
## -105.649 -24.061 -3.601 19.862 238.167
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 145.7684 9.4701 15.393 < 2e-16 ***
## age -0.1729 0.1106 -1.563 0.118099
## nonwhiteyes 4.0728 2.2751 1.790 0.073544 .
## smokingyes 3.1098 2.1670 1.435 0.151386
## drinkanyyes -2.0753 1.4666 -1.415 0.157168
## BMI 0.5821 0.1601 3.636 0.000282 ***
## statinsyes 3.8081 7.8249 0.487 0.626536
## BMI:statinsyes -0.7019 0.2694 -2.606 0.009215 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 36.8 on 2737 degrees of freedom
## (16 observations deleted due to missingness)
## Multiple R-squared: 0.05522, Adjusted R-squared: 0.0528
## F-statistic: 22.85 on 7 and 2737 DF, p-value: < 2.2e-16- Is there a relationship between LDL cholesterol and BMI or any of the other lifestyle and demographic variables, age, ethnicity, smoking, statin use or alcohol use?
This question can be answered using the ANOVA F-test. The hypothesis for this test are
\[H_0:\;\beta_{age}=\beta_{nonwhite}=\beta_{smoking}=\beta_{BMI}=\beta_{statins}=\beta_{BMI*Statins}=0\;\text{ vs }\;H_1:\text{ At least one $\beta_j\neq 0$}\]
The F statistic is 22.85 with a p-value of \(<0.0001\). So there is signifcant evidence that there is a relationsip with LDL cholesterol levels and at least one of the variables BMI, age, ethnicity, smoking, statin use, or alcohol use.
- How strong is the relationship?
\(R^2\) gives a measure of the predicitive power of the model. This model has an \(R^2\) of 5.52%, so 5.52% of the variation in LDL cholesterol levels are explained by BMI, age, ethnicity, smoking, alcohol use, and statin use. This is a fairly low $R^2% value. We do have several predictors that are not significant in the output including age, smoking, and alcohol use. What we do with these variables is part of the variable selection problem that we will explore in the next week. If our goal is to predict LDL cholesterol levels, then we could drop these variables in some order to see if the model improves (how we do this is the topic of next week). If our goal is to study the relationship between say BMI and LDL, then we may want to keep these variables in the model any as potential confounders.
- Does age have an affect on LDL cholesterol levels?
For age to have an effect on LDL cholesterol levels, its slope parameters should be non-zero. To answer this question, we can use the t-test for \(\beta_{age}\) by testing
\[H_0:\;\beta_{age}=0\;\text{ vs }\;H_1:\;\beta_{age}\neq 0\].
The test statistic for this test is \(t=-1.53\) with a p-value of 0.1181. With a p-vale of 0.1181, we do not have evidence that the slope for age is different from zero at the 0.05 alpha level, controlling for BMI, race, smoking, alcohol and statin use. Therefore, we do not believe that age has a significant effect on LDL cholesterol.
- How large is the effect of age on LDL cholesterol levels?
We can use a confidence interval for \(\beta_{age}\) to answer this question. The 95% confidence interval for \(\beta_{age}\) is (-0.39,0.04).
We are 95% confident that for each one year increase in age, there is between a 0.39 derease to a 0.04 mg/DL increase in mean LDL cholesterol levels, controlling for the other predictors. Note that this confidence interval includes zero, so there is no significant change in the mean cholesterol level due to age.
- What is the LDL cholesterol level for some one who takes statins, does not drink or smoke, is 65 years old, is nonwhite, and has a BMI of 24? How accurate is this estimate?
The best estimate we can make is by calculating the estimate mean LDL cholestorl level for someone with these predictor values, that is, calculate the \(\hat{y}\) for these predictor values. To asses the accuracy, we need a prediction interval, since we are intersted in the estimated LDL for an individual. These are given in the output below.
## fit lwr upr
## 1 139.5382 67.19006 211.8863Below is how we would manully calculate the estimate mean LDL level for these predictor values. We would plug the predictor values into the estimated regression function.
\[\hat{y}=145.8-0.17*65+4.07*0+3.11*0-2.08*0+0.58*24+3.81*1-0.70*24*1=139.5\]
The predicted LDL cholesterol level for a femal who is 65 years old with a BMI of 24 who is non-white, uses statins, and doesn’t smoke or drink alcohol is 139.54 mg/dL. This is just an estimate based in the data. To truly make a valid inference on this LDL level, we need to use a confidence interval, which in this case is a prediction interval. We are 95% confident that the mean LDL cholester level for a female who is 65 years old with a BMI of 24 who is non-white, uses statins, and doesn’t smoke or drink alcohol is between 67.16 mg/dL to 211.89 mg/dL.
- Is the effect of BMI on LDL cholesterol different between subjects that take statins and those that dont?
This question is about the interaction effect between BMI and statin on LDL cholesterol levels. To test this claim, we need to test the slope for the interaction term, \(\beta_{56}\). The t-test for this parameter is
\[H_0:\;\beta_{BMI*Statins}=0\;\text{ vs }\;H_1:\;\beta_{BMI*Statins}\neq 0\].
The test statistic is \(t=-2.606\) with a p-value of 0.009215. With a p-value of 0.009215, we have very strong evidence that the slope for the interaction term is non-zero at the 0.05 alpha level, adjusting for the other predictors. This means that we do have significant evidence that the effect of BMI on LDL cholesterol is different between statin and non statin users in females.
- Is there a linear relationship between LDL and the other variables?
This question is asking us to check whether our model meets the linearity assumption. To assess this, we can look at a scatterplot of the residuals vs fitted values.
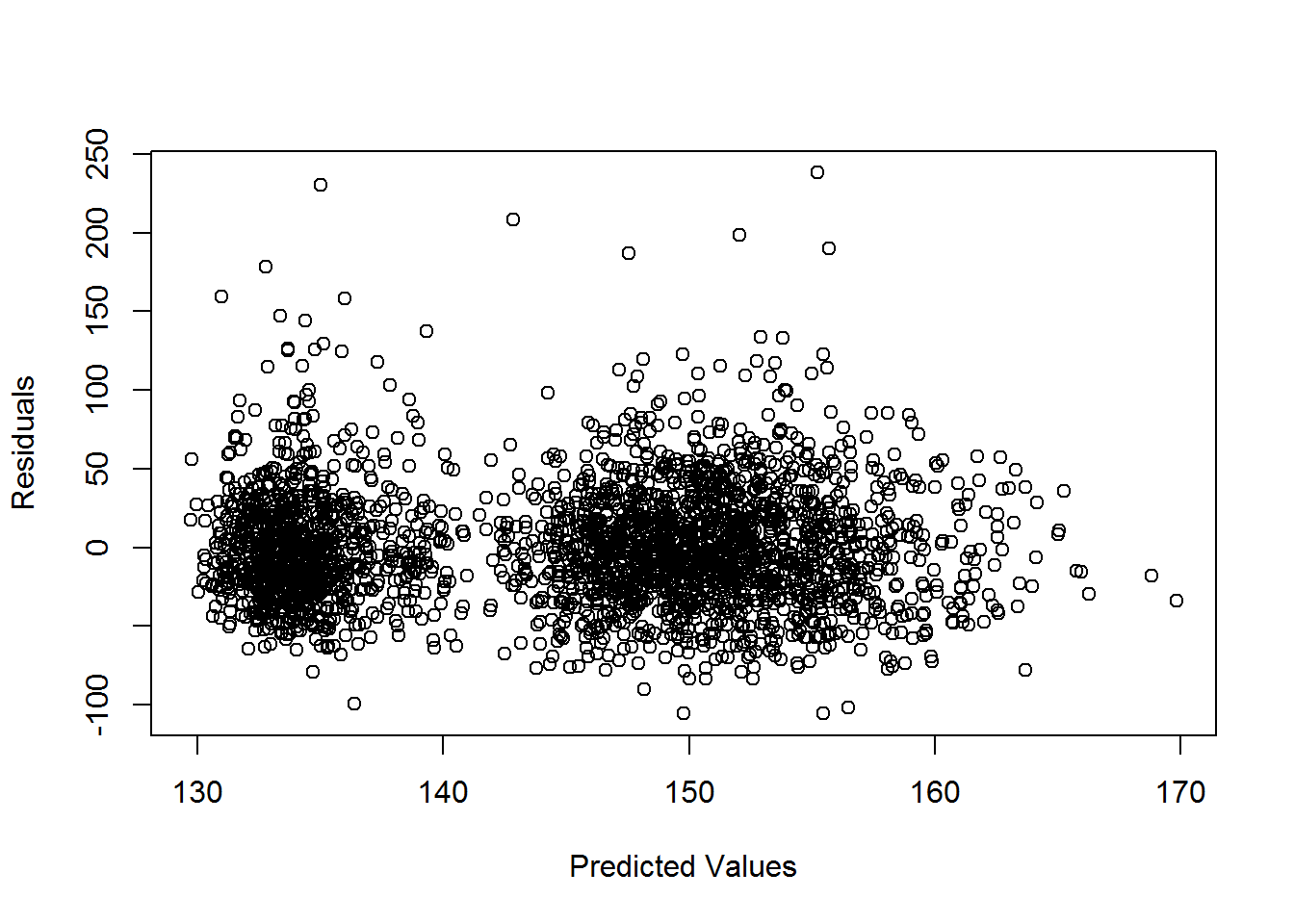 Looking at the scatterplot, there is no evidence of non-linearity, so yes the relationship does appear to be linear between the response and the predictors.
Looking at the scatterplot, there is no evidence of non-linearity, so yes the relationship does appear to be linear between the response and the predictors.
While we are here, let’s examine the other assumptions. Again looking at the plot of residuals vs predicted values, there does not seem to be any evidence of non constant variance. There do appear to be a few potential outliers.
For the normal errors assumptions, we can examine the histogram and QQ plot of the residuals given below.
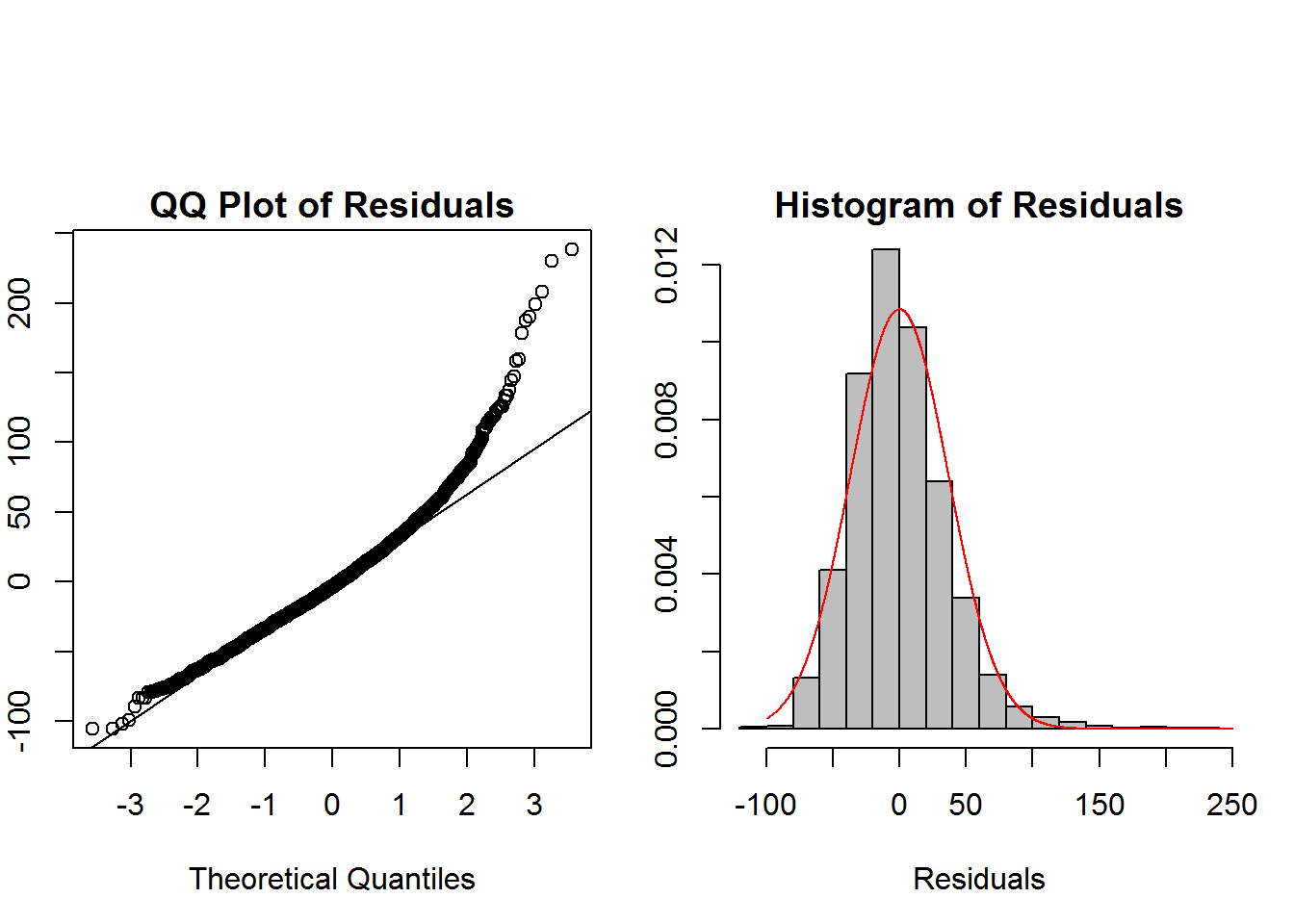 There appears to be some skewness to the right for the residuals, but it is not so heavy that it will be a problem. This may be due to the potential outliers seen in the plot of residual vs predicted values. The large sample size here will help with these slight deviations from the model assumptions. A log transform of the response may also help adjust for the skewness.
There appears to be some skewness to the right for the residuals, but it is not so heavy that it will be a problem. This may be due to the potential outliers seen in the plot of residual vs predicted values. The large sample size here will help with these slight deviations from the model assumptions. A log transform of the response may also help adjust for the skewness.
The subjects for this study were initially randomized to a hormone treatment, so it would be reasonable to assume that the subjects are independent. We may still want to examine the study sample for clusters.