Some Examples: Simple Linear Regression

Let’s take a look at some examples, so we can get some practice with these interpretations.

Example 1. The skin cancer data set contain 49 observations on skin cancer mortatlity rates by state with the latitude (North/South position) at the center of the state. Let

$y=\text{skin cancer mortatility rate}$
$x=\text{Latitude at the center of the state}$

We should always start by exploring our data with plots. In this case, since we are interested in regression, we need to make a scatterplot to see if there is an approximately linear relationship.

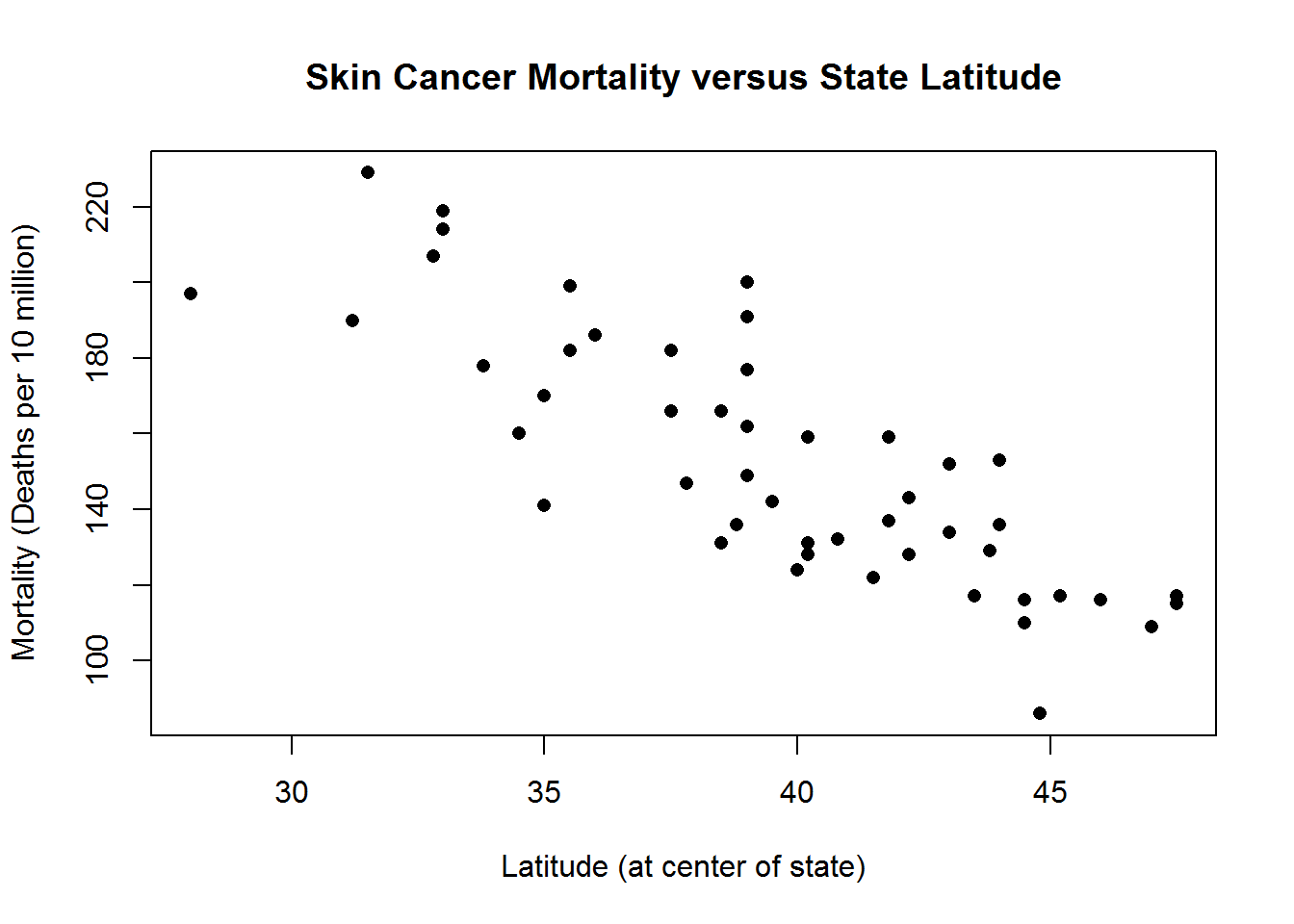The scatterplot looks reasonably linear with a negative slope, so linear regression is appropriate. As latitude increases, the skin cancer mortality rate tendss to descrease. The following output is from R, where we fit the simple linear regression model

\[\widehat{Moratlity}=\beta_0+\beta_1Latitude\]

## 
## Call:
## lm(formula = Mort ~ Lat, data = skin.dat)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -38.972 -13.185   0.972  12.006  43.938 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 389.1894    23.8123   16.34  < 2e-16 ***
## Lat          -5.9776     0.5984   -9.99 3.31e-13 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 19.12 on 47 degrees of freedom
## Multiple R-squared:  0.6798, Adjusted R-squared:  0.673 
## F-statistic:  99.8 on 1 and 47 DF,  p-value: 3.309e-13

## [1] "r =  -0.825"

The estimated regression equation is $\widehat{Mort}=389.19-5.98Lat$ with $R^2=67.98\%$ and correlation coefficient $r=-0.825$.

The interpretation of the slope ($\beta_1=-5.98$) is the mean skin mortality rate is estimated to decrease by 5.98 deaths per 10 million for each one degree increase in latitude.
The interpretation of the y-intercept ($\beta_0=389.19$) is the mean skin mortatlity rate for states at a latitude of 0 degrees is 389.19 deaths per 10 million. Since there are no states at or near a latitude of 0, the interpretation of the y-intercept is not practically meaningful.
The correlation ($r=-0.825$) is negative and close to -1, so this tells us that the linear relationship is negative and reasonable strong.
With an $R^2$ of 67.98%, we can say that 67.98% of the variation in skin cancer mortality rates is explained by latitude.

Example 2: Teen Birth Rate and Poverty Level Data. This dataset contains 51 observations for the 50 states and Washington D.C. The variables are

$y=\text{the birth rate per 1000 females 15 to 17 years old in 2002}$
$x=.

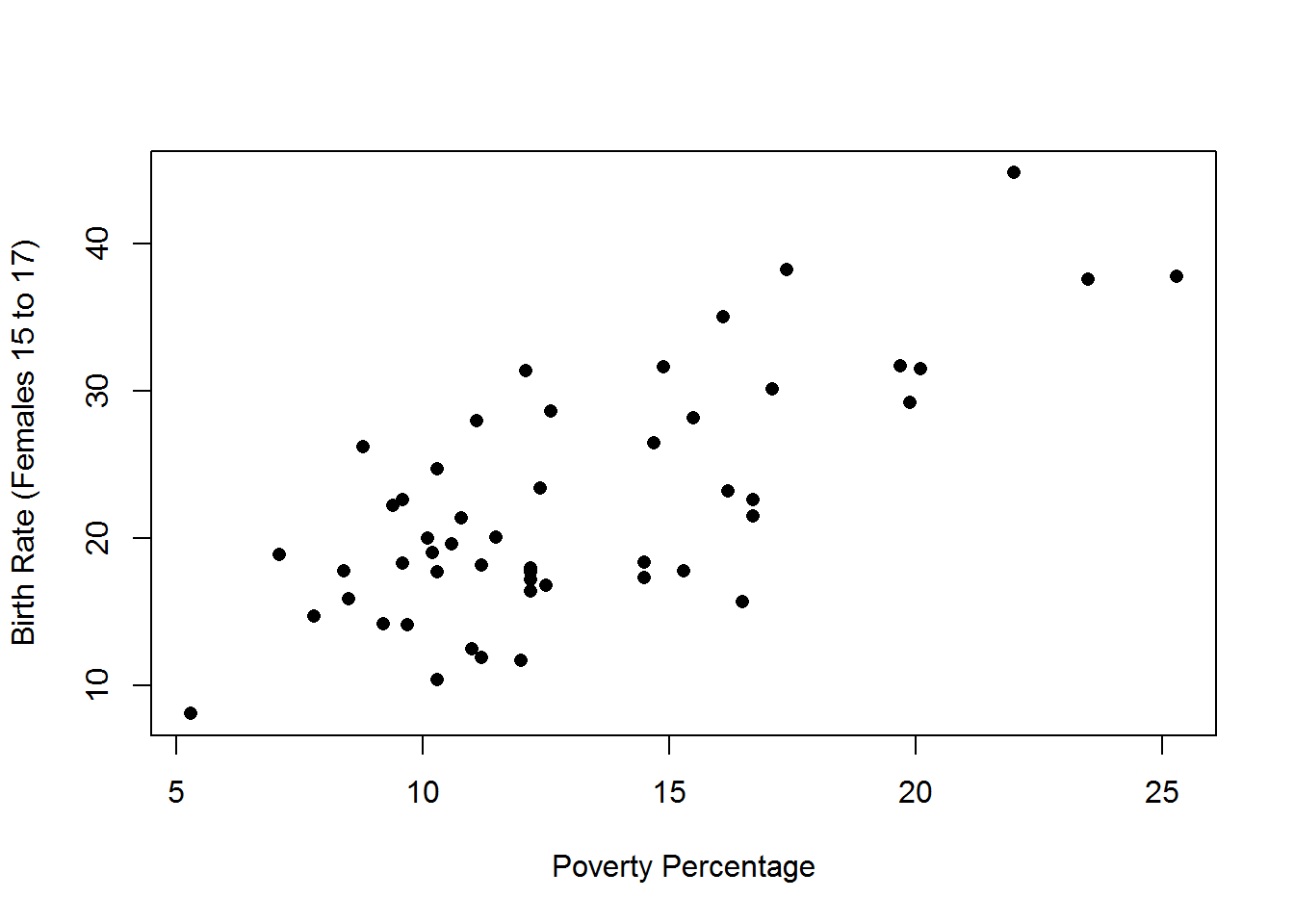
The plot of the data below shows that the relationship is reasonably linear with a positive slope. As poverty level increases, the birth rate for 15 to 17 year old females tends to increase.

The output below if for the linear regression model

\[\widehat{Birth Rate}=\beta_0+\beta_1Poverty.\]

## 
## Call:
## lm(formula = Brth15to17 ~ PovPct, data = poverty.dat)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -11.2275  -3.6554  -0.0407   2.4972  10.5152 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   4.2673     2.5297   1.687    0.098 .  
## PovPct        1.3733     0.1835   7.483 1.19e-09 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 5.551 on 49 degrees of freedom
## Multiple R-squared:  0.5333, Adjusted R-squared:  0.5238 
## F-statistic:    56 on 1 and 49 DF,  p-value: 1.188e-09

## [1] "r =  0.7303"

The estimated regression equation is $\hat{y}=4.267+1.373x$ with $R^2=53.33\%$ and $0.7303$.

The interpretation of the slope ($\beta_1=1.373$) is that the mean 15 to 17 year old birth rate is estimated to increase by 1.373 births per 1000 females age 15 to 17 for each 1% increase in the poverty rate.
The interpretaion of the y-intercept ($\beta_0=4.267$) is that the mean birth rate for 15 to 17 year old females is estimated to be 4.267 births per 1000 females aged 15 to 17 for states with 0% poverty. Since there were no states with a poverty rate of 0%, this interpretation in not practically meaningful.
$R^2=53.33%: 53.33% of the variation in birth rate for 15 to 17 year old females is explained by poverty rate.
The correlation coefficient, $r=0.7303$, indicates that the linear relationship between poverty rate and birth rate for 15 to 17 year old females is positive, as poverty rate increases the birth rate tends to increase, and has moderate strength.

Learn By Doing: Lung Function in 6 to 10 Year Old Children

This dataset contain 345 observations on children between 6 and 10 years old. The variables are

$y=\text{forced exhalation volume (FEV), a measure of how much are someone can forcibly exhale from their lungs}$
$x=\text{age in years}.$

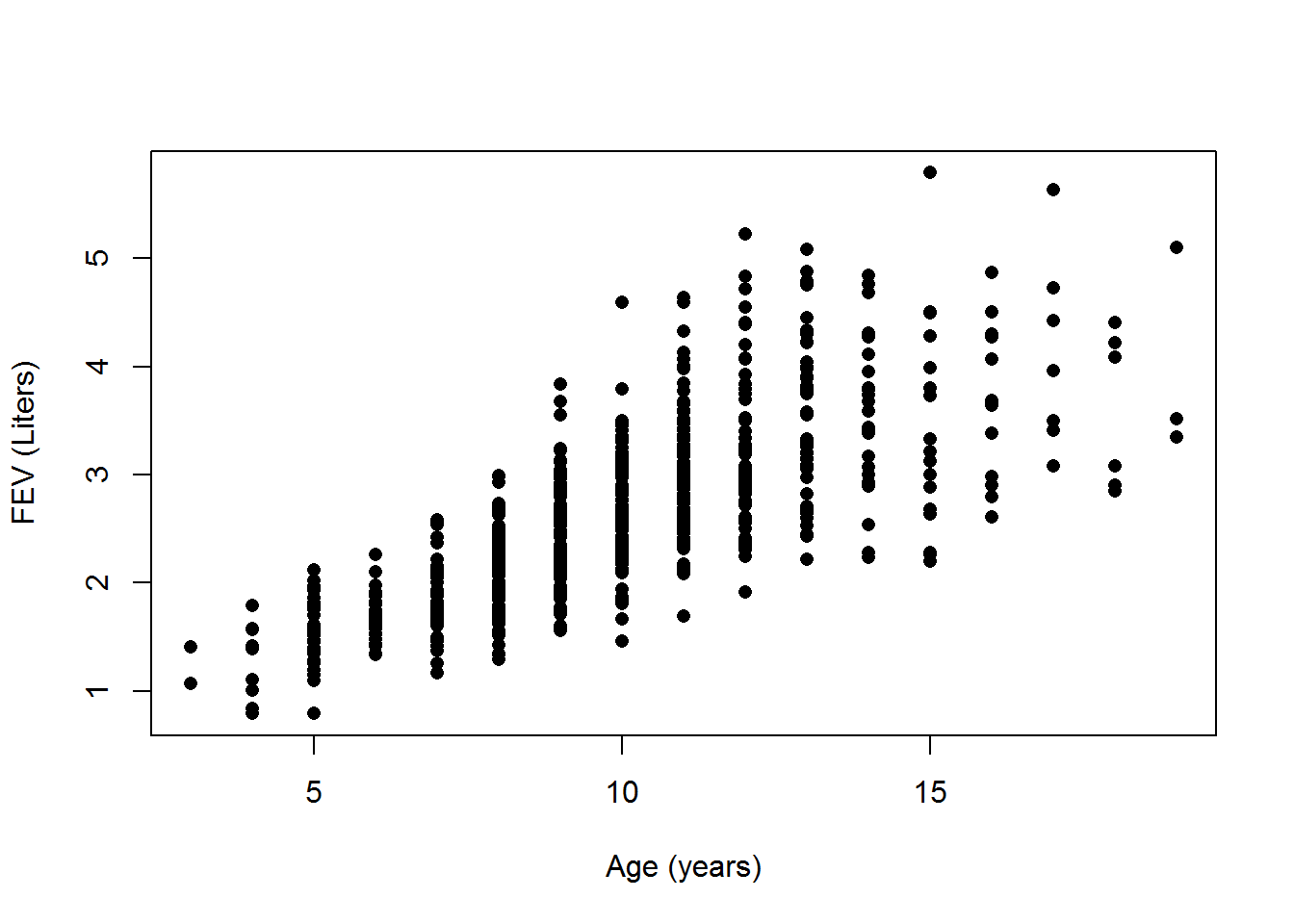
Below is a scatterplot of age vs FEV along with the simple linear regression output. Use this output to answer the following questions.

## 
## Call:
## lm(formula = FEV ~ age, data = fev.dat)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -1.57539 -0.34567 -0.04989  0.32124  2.12786 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 0.431648   0.077895   5.541 4.36e-08 ***
## age         0.222041   0.007518  29.533  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.5675 on 652 degrees of freedom
## Multiple R-squared:  0.5722, Adjusted R-squared:  0.5716 
## F-statistic: 872.2 on 1 and 652 DF,  p-value: < 2.2e-16

## [1] "r =  0.7565"

The estimated regression equation is $\hat{y}=0.432 + 0.222x$ with $R^2=57.22\%$ and $r=0.7565$.

Is linear regression appropriate?
Interpret the slope.
Interpret the y-intercept. Does the y-intercept interpretation make sense?
Interpret $R^2$.
Interpret Pearson’s correlation coefficient, $r$.

Solutions